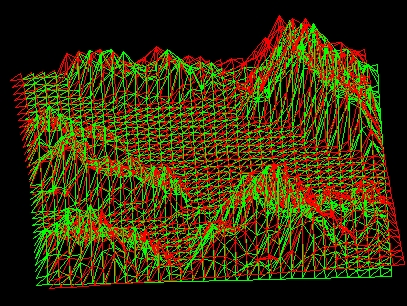
L'algoritmo che permette di visualizzare le immagini che vedete si basa sulla ripetizione di questi passaggi: - 1)Disegna una serie di quadrati o rettangoli, 2) dividili tutti con una diagonale in modo da formare 2 triangoli rettangoli con ogn'uno di loro. 3) unisci almeno 4 quadrati e solleva la loro parte centrale.
Sollevando a varie altezze i vertici di molti di questi 4 quadrati, si crea un'illusione particolare, i poligono così disposti sembrano montagne più o meno alte, oppure colline.

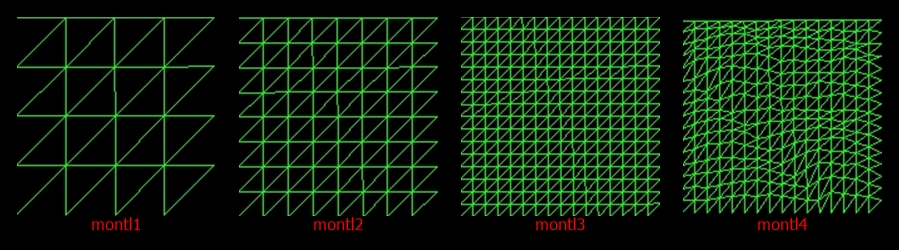
Figura 1: - Si parte da un rettangolo diviso da una diagonale. Figure 2, 3, 4; - Si uniscono e...


A questo punto basta regolare le altezze e la frequenza dei vari picchi in un modo casuale, ma entro certi limiti scelti dal programmatore, questo permette di avere una varietà di paesaggi
Bastano pochi poligoni per avere un effetto montagna.

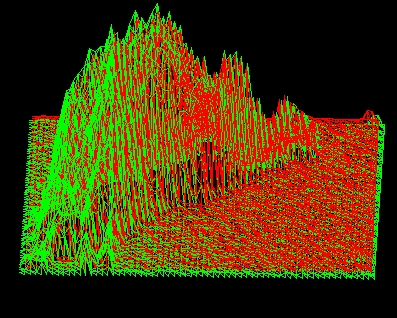
Naturalmente l'unione di un maggior numero di poligoni rende meglio la simulazione.
Le due immagini qui sopra, oltre ad avere una dimensione maggiore sono più definite. La scelta di usarne solo 2 è dettata dal fatto che richiedono molto tempo per essere visualizzate quando la pagina viene richiamata.

Queste immagini sono formate da triangoli vuoti sono esteticamente meno belle ma rendono meglio l'idea di come l'incontro dei vertici dei poligoni siano sollevati.
Nella prossima pagina vi mostrerò come la sovrapposizione di una stessa immagine leggermente decentrata e colorata diversamente, possa generare un effetto stereografico.
L'algoritmo che ho usato nell'applet con il quale ho ottenuto queste immagini l'ho trovato in rete ed è del
Sig. Evgeny Demidov
ricercatore Senior (CHC)
Semiconductor dipartimento di fisica dell'Istituto di Fisica di microstrutture RAS Nizhny Novgorod, Russia.
TERNE PITAGORICHE
Conosciuta come terna Pitagorica per il chiaro rapporto con l'omonimo teorema, X2 + Y2 = Z2 la soluzione per trovare 3 numeri che soddisfacevano l'equazione
era già nota ai tempi di Diofanto
Ad esempio 32 + 42 = 52
è una terna pitagorica, e da questa se ne possono formare infinite altre, basta moltiplicare ogn'uno di questi tre numeri per un numero qualsiasi N > 0 per averne un'altra, se ad esempio li moltiplichiamo per 2 avremo 62 + 82 = 102
oppure se li moltiplichiamo per 5 avremo 152 + 202 = 252
Ma solo la prima viene chiamata terna pitagorica primitiva, perchè i numeri 3,4 e 5 non hanno fattori comuni mentre quelle ottenute con il numero moltiplicatore N hanno evidentemente in comume il fattore N come nel nostro esempio 6,8,e 10 hanno in comune il fattore 2, un'altra terna primitiva ad esempio e quella formata dai numeri 5, 12 e 13, perchè non ha fattori comuni.
La formula per generare tutte le terne pitagoriche primitive è (x= 2*s*t,
y= s2 - t2
z= s2 + t2 )
Dove (s) e (t) sono numeri naturali qualsiasi superiori a zero e (s) è maggiore di (t) inoltre (s) e (t) non non devono avere un fattore in comune e per finire uno deve essere pari e l'altro dispari.
Se ad esempio s= 3 e t= 2, allora x= 12, y= 5 e z= 13
Questa soluzione era contenuta negli ELEMENTI
di Euclide ma era nota anche ai tempi di Diofanto e se ne trova una versione nella tavoletta babilonese, Plimpton 322.
Una formula più facile da ricordare è la prossima, perchè utilizza solo un numero iniziale per generare la terna.
Se abbiamo come seme un numero dispari n =3
, allora
z= (n2+1)/2,
perciò z= (3*3+1)/2 = 5, x= (n2-1)/2
ossia x= = (3*3-1)/2 = 4, y= al seme n= 3
. Una terna primitiva.
Se abbiamo come seme il numero n =4
Cioè un numero pari, allora
z= (n2+1),
perciò z= (4*4+1) = 17, x= (n2-1)
ossia x= (4*4-1) = 15, y= seme *2 = 8
Una terna primitiva.
Con i numeri pari esiste anche questa variante:-
Se abbiamo come seme il numero n =8
z= (n2/4)+1,
perciò z= (8*8/4)+1 = 17, x= (n2/4)-1
ossia x= (8*8/4)-1 = 15, y= seme 8
Una terna primitiva come la precedente ma che richiede anche 2 divisioni, inoltre questa formula fornisce terne primitive solo con il numero 4 ed i suoi multipli
Se abbiamo un 6 come seme avremo 10 - 8 - 6 con 2 come fattore comune.
Avrete notato che in queste ultime formule le terne che utilizzano un numero dispari come seme, hanno i 2 numeri maggiori che sono consecutivi, mentre quelle che utilizzano un numero pari hanno i numeri maggiori divisi da 2 unità
Notiamo inoltre che la terna che utilizza un numero dispari come seme
avrà come somma dei 2 numeri maggiori un numero quadrato, ad esempio con la terna 3 -4 -5 la somma 4+5= 9 che è il quadrato di 3, oppure la terna 5 -12 -13 con (12+13 = 25) che è il quadrato di 5 ovvero il quadrato del seme utilizzato per generarle.
Un' altra formula che utilizza un numero generatore n pari
è a= 1+n2, b= a-2, c= (a+b)/n
se ad esempio abbiamo n= 6 avremo x= 37, y= 35 e z= 12, una terna primitiva.
Come vedi formule per ottenere terne pitagoriche ce ne sono varie, ma la più originale che mi è capitato di vedere è quella che utilizza i numeri della serie di Fibonacci, 1-1-2-3-5-8-13-21-34-55-89...
se prendiamo 4 numeri consecutivi di questa serie, ad esempio 3-5-8-13
e motiplichiamo tra loro i due numeri esterni (3*13 =) 39 e se poi raddoppiamo il prodotto dei due numeri interni, (5*8*2 =)80 avremo i due numeri minori della terna 39-80-89 Il numero 89 è il risultato della radice quadrata di 392 + 802 = 7921 = 89 inoltre appare notevole il fatto che oltre ad essere anche 89 un numero della serie, il suo pedice è la metà della somma dei 4 pedici di partenza, la somma dei 4 pedici corrispondenti ai 4 numeri 3-5-8-13 sono sono 4+5+6+7= 22 mentre 89 corrisponde all'11 numero della serie,
controlla qui sopra.
Biblio
Numeri Memorabili dizionario di numeri matematicamente curiosi - di David Wells ed. Zanichelli
Dove va la matematica - di Keith Devlin ed. Bollati Boringhieri
103 Curiosità Matematiche - di G.Balzarotti e P Lava ed. Hoepli.
Sito http://www.fq.math.ca/ dell'Associazione Fibonacci, Il Fibonacci Quarterly