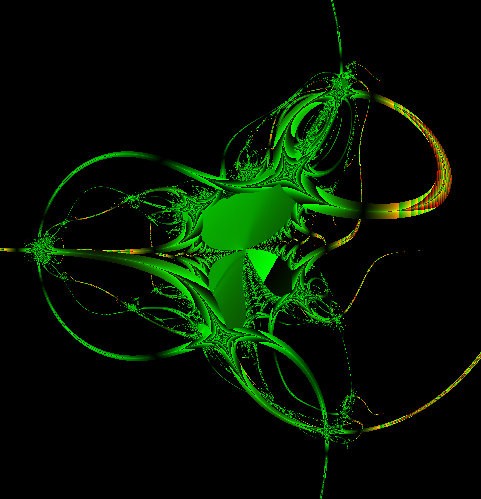
img. 9
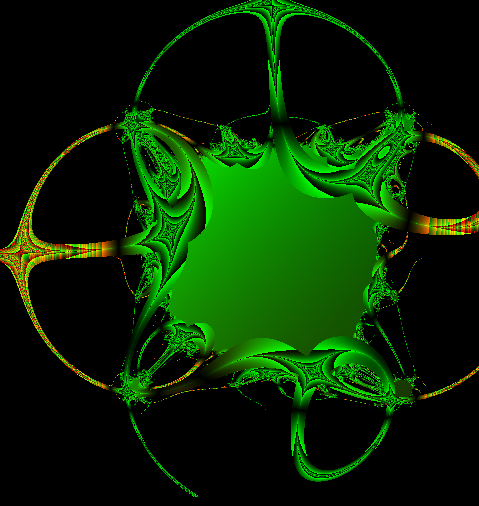
img. 10
La prima di queste due immagini sopra Ŕ generata dall'equazione x^3 - 1 =0 mentre la seconda da x^4 -1=0, evidentemente in queste due immagini l'equazione ha subito dei cambiamenti che hanno mirato non a risolvere l'equazione in un modo migliore, ma a portare dei risultati grafici esteticamete interessanti.
img. 11
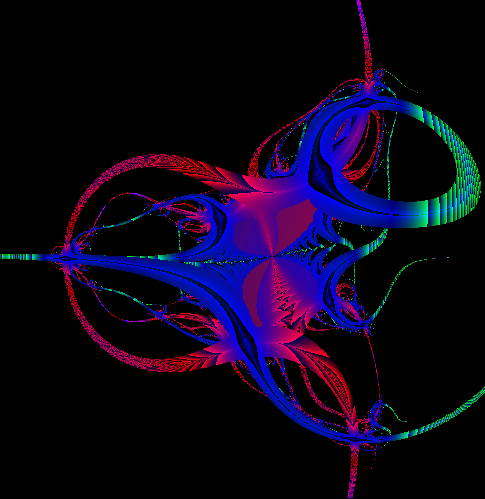
img. 12
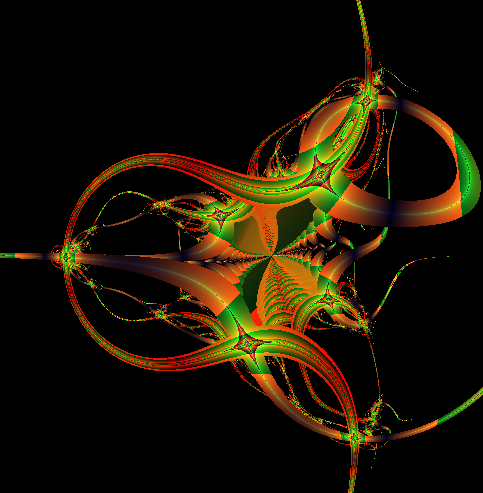
img. 13

img. 14

Le immagini num. 11 e 12 sono diverse solo per i valori cromatici in quanto hanno la medesima radice cubica e lo stesso algoritmo.
La num. 13 Ŕ un ingrandimento di una radice cubica mentre la num.14 Ŕnasce da una radice quadrata.
img. 15

img. 16

img. 17

img. 18

Le immagini num. 15, 16 e 18 hanno la medesima radice quarta .
La num. 17 Ŕ una radice cubica.
img. 19

img. 20

img. 21

img. 22

Dalla num. 19 in poi sono tutti ingrandimenti di varie radici
img.23

img. 24

A questo punto spero che la particolare bellezza di queste immaggini stimolino la vostra curiositÓ e vi spingano a realizzarne di vostre, alle pagine 6 e 7 ci sono i listati degli applet con cui ho realizzato la maggior parte di quelle che avete visto fin'ora.












 img. 9
img. 9
 img. 10
img. 10













