L'algoritmo per ottenere queste immagini l'ho già illustrato nella sezione riguardante le istruzioni per apprendere l'essenziale del linguaggio di programmazione Java per ottenere un insieme di Mandelbrot.
Questo è il Capitolo iniziale
Per chi non ha interesse per la programmazione, più avanti troverete alcune informazioni su quello che per me è una fonte di immagini spettacolari sempre nuove e misteriose
Questo è il Capitolo iniziale
Per chi non ha interesse per la programmazione, più avanti troverete alcune informazioni su quello che per me è una fonte di immagini spettacolari sempre nuove e misteriose


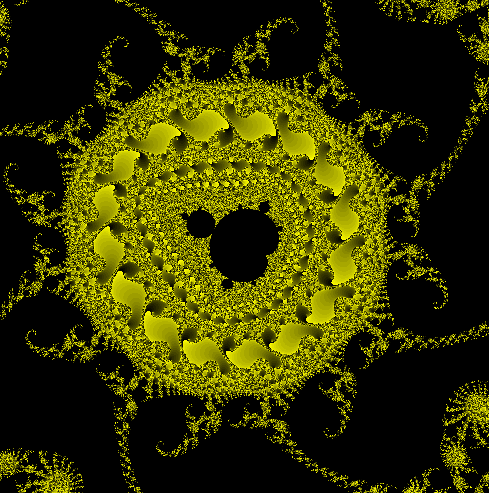
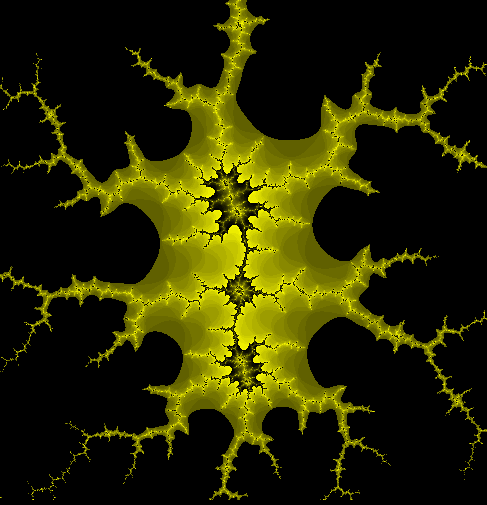
Nella prima immagine a sinistra si vede un'immagine dll'insieme di Mandelbrot realizzata in un modo che crea un effetto di profondità.
I punti che appartengono all'insieme di M. sono solo quelli colorati in nero, gli altri sono quelli che superato il suo confine, tendono ad allontanarsi sempre più velocemente, i colori vengono assegnati in base alla velocità con cui si allontanano dal confine, in altri termini, minore è il numero delle iterazioni necessarie alla formula per superare il confine, maggiore è la velocita di fuga, se per esempio servono solo 10 iterazioni si assegna il colore rosso, se occorrono 20 iterazioni il pixel in esame si colora di blu, etc.
Nell'immagine a destra viene evidenziata la zona che presenta i risultati più spettacolari della formula, è situata subito dopo il confine nero , in questa zona di confine la formula presenta un andamento strano nel senso che sembra avere difficoltà nel decidere se un risultato debba restare dentro il confine nero o uscirne, è questa indecisione che determina il numero delle iterazioni della formula che a sua volta stabilisce il colore del pixel e che alla fine forma dell'immagine finale.
I punti che appartengono all'insieme di M. sono solo quelli colorati in nero, gli altri sono quelli che superato il suo confine, tendono ad allontanarsi sempre più velocemente, i colori vengono assegnati in base alla velocità con cui si allontanano dal confine, in altri termini, minore è il numero delle iterazioni necessarie alla formula per superare il confine, maggiore è la velocita di fuga, se per esempio servono solo 10 iterazioni si assegna il colore rosso, se occorrono 20 iterazioni il pixel in esame si colora di blu, etc.
Nell'immagine a destra viene evidenziata la zona che presenta i risultati più spettacolari della formula, è situata subito dopo il confine nero , in questa zona di confine la formula presenta un andamento strano nel senso che sembra avere difficoltà nel decidere se un risultato debba restare dentro il confine nero o uscirne, è questa indecisione che determina il numero delle iterazioni della formula che a sua volta stabilisce il colore del pixel e che alla fine forma dell'immagine finale.
img. 3


img. 4


Nella prima immagine a sinistra si vede quello che assomiglia un cavalluccio marino, mentre quella a destra è la stessa immagine ma senza gli avallamenti che la circondano in questo modo si evidenza la parte più interessante.
img. 5


img. 6


La num. 5 è un ulteriore ingrandimento delle due immagini precedenti, notate il piccolo insieme di M. al centro dell'immagine, queste repliche dell'insieme di M. sono sparse ovunque all'esterno del bordo nero dell'insieme originale, anche se sono molto simili non sono esattamente identiche inoltre la loro distribuzione non è omogenea o regolare come nei frattali normali.
L'mmagine a destra presenta una doppia spirale di figure che sembrano ricami di merletti.
L'mmagine a destra presenta una doppia spirale di figure che sembrano ricami di merletti.
img. 7


img. 8

La num. 7 e num. 8 sono due altri ingrandimenti che presentano al loro centro un altro insieme di M. se si ingrandiscono questa immagini si vedrebbero altri insiemi come questi che a loro volta se ingranditi presenterebbero altre repliche simili all'originale, questo processo è limitato solo dalla potenza di calcolo del computer.
img. 9


img. 10

La num. 9 Sembra un'isola che nasconde al suo interno un insieme di M. ed è circondata da 4 linee che hanno all'estremità altre isole all'ungate, con all'interno dei punti scuri, l'immagine num. 10 è un ingrandimento di una delle quattro isole allungate, notate che al suo interno nasconde delle parti scure che hanno al loro interno altre repliche del disegno originale, che se ingrandite ulteriormente mostrerebbero un altro insieme di M.
img. 11


img. 12

La figura num. 11 sembra una spirale di cavallucci marini mentre num. 12 è un'isola di forma quadrata, sempre circondata di cavallucci.
img. 13

img. 14

La figura num. 13 e la num. 14 sono una variazione sul tema, ma mi sembravano esteticamente interessanti.
La num.
img. 15


img. 16


La num. 15 e 16 sono simili alla 12 e alla 10 ma in questo caso ho messo in evidenza i contorni in modo da creare un effetto di profondità
img.17


img. 18


La num. 17 è un'altra bella immagine.
La num. 18 presenta una serie inversa di ingrandimenti, ossia si parte da un forte ingrandimento e con vari passaggi si arriva al punto iniziale che mostra le coordinate iniziali delle immagini.