img. 1


img. 2


Queste sono immagini che oltre al numero d'iterazioni della formula, prendono in cosiderazione anche la parte reale ed immaginaria del numero complessso legato al pixel in esame, la combinazione di questi tre parametri crea delle immagini molto pi¨ spettacolari di quelle che usano solo il numero di iterazioni dell'algoritmo, usando tre parametri invece di uno, si crea in alcune immagini un effetto di profonditÓ che le rendono quasi tridimensionali.
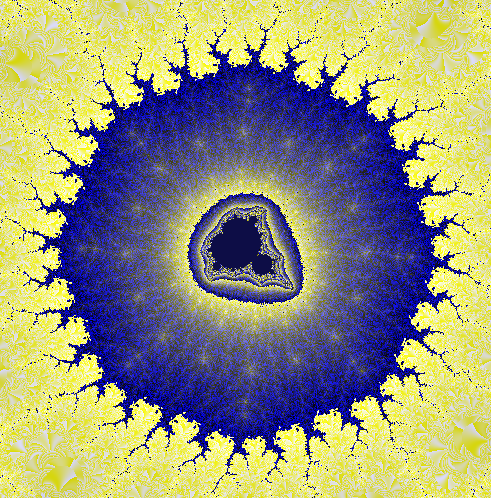
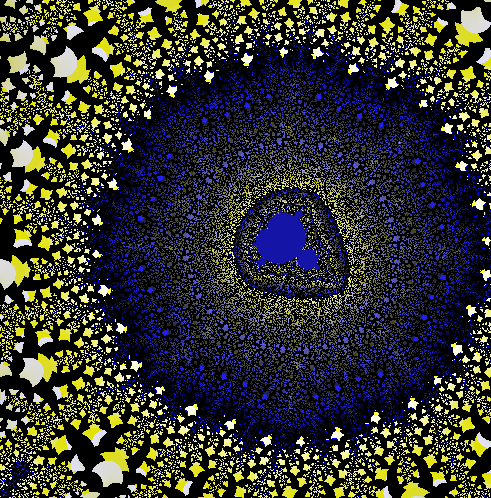
Questo accorgimento ha come conseguenza che alcune zone che appartengono all'insieme di M. che normalmente vengono colorate di nero, appaiono colorate come nelle immagini num.2 e num. 4
Questo accorgimento ha come conseguenza che alcune zone che appartengono all'insieme di M. che normalmente vengono colorate di nero, appaiono colorate come nelle immagini num.2 e num. 4
img. 3


img. 4


Un altro effetto dell'uso dei tre parametri Ŕ la possibilitÓ di variare di molto l'aspetto della stessa immagine, ad esempio le immagini num.1 e num.3 rappresentano la stessa zona del piano complesso, notate l'insieme di M. appena visibile al centro delle due immagini colorato di nero, oppure i colori metallici della num.4 rispetto a quelli della num.2
img. 5


img. 6

La num. 5 e la num.8 cosý come la num.6 e la num.7 sono due ulteriori esempi di come sia possibile variare l'aspetto finale di una immagine usando tre parametri.
img. 7

img. 8


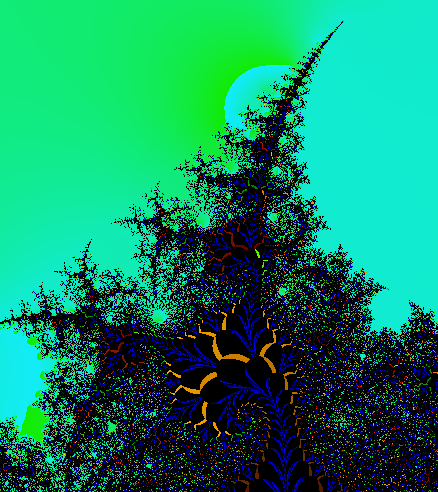
Le immagini dal num. 7 al num. 16 sono solo alcuni esempi di come sia possibile realizzare delle immagini molto particolari variando la combinazione dei tre parametri visti prima, in pratica si possono realizzare migliaia di immagini diverse per ogni punto del piano preso in esame e dato che i punti del piano complesso sono infiniti si possono realizzare infinite immagini diverse di questo insieme.
Indubbiamente insieme alla bellezza delle immagini, L'insieme di M. offre la possibilitÓ di intravedere l'infinito in uno spazio finito, che come noto Ŕ una delle prerogative che solo la matematica pu˛ offrire.
Indubbiamente insieme alla bellezza delle immagini, L'insieme di M. offre la possibilitÓ di intravedere l'infinito in uno spazio finito, che come noto Ŕ una delle prerogative che solo la matematica pu˛ offrire.
img. 9


img. 10


img. 11


img. 12


img. 13


img. 14


La num.
img. 15

img. 16


img.17


img. 18


Ma cosa succede se variamo la potenza di Z se ad esempio invece di z^2 usiamo Z^3 o Z^4 etc.
Rivediamo con l'immagine num. 17 l'esito che si ha con Z^2 che conosciamo giÓ, proseguiamo con l'immagine num.18 vediamo il risultato di Z^3 +c, naturalmente anche questa immagine pu˛ essere sottoposta ad ingrandimenti come la prima e che mostreranno al loro interno degli insiemi di M. che avranno l'aspetto dell'insieme di Z^3.
Nella pagina seguente vedrete i diversi aspetti che prendono gli insiemi di M. al variare delle potenza utilizzata nella formula.
Rivediamo con l'immagine num. 17 l'esito che si ha con Z^2 che conosciamo giÓ, proseguiamo con l'immagine num.18 vediamo il risultato di Z^3 +c, naturalmente anche questa immagine pu˛ essere sottoposta ad ingrandimenti come la prima e che mostreranno al loro interno degli insiemi di M. che avranno l'aspetto dell'insieme di Z^3.
Nella pagina seguente vedrete i diversi aspetti che prendono gli insiemi di M. al variare delle potenza utilizzata nella formula.